Type-safety 란 무엇인가

이번 포스팅은 이 글을 번역했습니다.

타입 안정성이란 무엇인가?

메모리 안정성을 정의하다(C 언어)라는 이전 포스팅에 이어, 댓글에 누군가가 타입 안정성에서도 다뤄보면 좋겠다는 얘길 했습니다. 타입 안정성이란 누구나 조금씩은 알고 있지만, 그것이 정확히 무엇인지 알기는 힘든 부분이 있습니다. 누가 ‘자바는 타입 세이프한 언어다’라고 할 때, 이게 과연 무슨 뜻일까요?모든 타입 세이프한 언어들은 어떤 면에서보면 동일하다고 할 수 있을까요? 특정 언어에 대한 타입 안정성이란 일반적으로 어떤걸 제공하는 걸까요?

타입 안정성이란 사실 언어의 타입 시스템의 정의에 따라 다른 의미를 갖습니다. 가장 단순한 경우는 타입 안정성이 프로그램의 잘 정의됨(well-defined)을 보장하는 것입니다. 더 일반적으로는 언어의 타입 시스템은 그 언어가 만들어내는 프로그램들의 정확성과 보안을 가능케 하는 강력한 도구이며, 이러한 새로운 타입 시스템을 만들어내는 것은 현재도 널리 연구되고 있습니다.

기본 타입 안정성

타입 안정성에 관한 직관적 해석은 다음 문장으로 짧게 표현될 수 있습니다. “잘 타입된 프로그램은 절대 잘못될 수 없다”(Well typed programs cannot go wrong). 1978년 발표된 로빈 밀너의 [프로그래밍에서의 타입 다형성에 관한 이론]에서 나온 말인데요, 이 문장을 파헤쳐 봅시다. 먼저 잘못될 수 없음에 대해서 논해보고자 합니다.

잘못되는 것에 관하여 (About Going wrong)

프로그래밍 언어들은 고유의 문법(syntax) - 무엇을 쓸 수 있는가 - 의미(semantics) - 프로그램들이 무엇을 뜻하는가에 의해 정의됩니다. 모든 언어들이 직면하는 문제는, 문법적으로는 옳지만 의미적으로는 문제가 많은 프로그램들이 많다는 것입니다. 노암 촘스키의 유명한 “색 없는 녹색 이상들이 난폭하게 잔다(Colorless green ideals sleep furiously)” 예시는 문법은 틀리지 않았으나 의미적으로 가치없는 대표적인 문장입니다. OCaml에서는 1+”foo”와 같은 코드가, C에서는 {char buf[4]; buf[4]=’x’}와 같은 코드가 비슷한 예시입니다. 할당되지 않은 공간인 buf[4]에 변수를 할당하는 것은 잘못되는 것의 예시입니다.

타이핑이 잘 되면 잘못될 수 없다

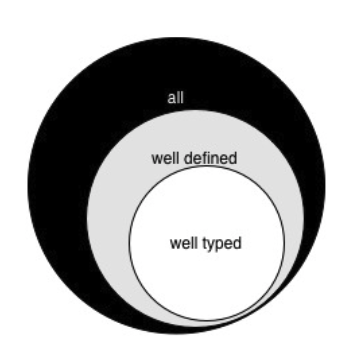
타입 안정성을 보장하는 언어에서는, 타입 시스템 자체가 잘못 되지 않음을 보장해줍니다; 혹은 타입 안정성이 프로그램을 잘못되게 하지 않을 때 타이핑이 잘 되었다 (well-typed)라고 말합니다. 타입 안정성을 보장하는 언어에서, well typed 는 well-defined의 부분집합입니다. 그리고 그 둘은 문법적으로 가능한 모든 프로그램의 부분집합입니다.

어떤 언어들이 타입 안정성을 보장할까?

C와 C++는 타입 세이프하지 않습니다: C의 표준 타입 시스템은 의미없는 코드들을 배제하지 않습니다. 예를 들면 버퍼의 끝에 적는 것 같은 행위들인데, 이런 것들 때문에 타이핑을 잘 한 C로 짠 프로그램들도 잘못될 수 있습니다. C++는 C의 초집합(superset)이므로 C의 속성을 따라간다고 볼 수 있습니다.

자바와 C#은 (아마도) 타입 세이프 합니다: 엄청 비대한 어떤 언어적 구현이 타입 세이프한지 판단하기는 꽤나 어렵지만(초기 버전의 자바 제너릭은 버그가 많았습니다), 작고 대표적인 언어에 대해서는 (featherweight Java) 그것이 가능합니다. 흥미롭게도 C의 의미론(semantics)에서 undefined로 된 부분에 대해 의미를 부여한다면, 타입 세이프하다고 할 수 있을 것 같습니다. 예를 들어 C에서는 배열 범위 밖의 원소에 접근하는 것이 의미가 없지만(meaningless), 자바나 C#에서는 ArrayOutOfBoundsException을 던지기 때문에 의미가 있습니다.

파이썬과 루비는 (논쟁의 여지가 있지만) 타입 세이프 합니다: 파이썬과 루비는 실행중 시그널 타입 에러에 대해 예외를 던지는 동적 타입 언어들로 소개되곤 합니다. 자바가 ArrayOutOfBoundsException을 던지듯, 루비도 integer와 string을 더할 때 예외를 던집니다. 위의 두 경우는 언어의 의미론적 관점에서 잘 정의된 (well-defined) 예시라고 할 수 있습니다. 사실 의미론은 모든 프로그램들에게 의미를 부여하기 때문에, 위의 well-defined를 가리키는 다이어그램과 다른 모든 다이어그램들은 동치입니다. 따라서 위 언어들은 null 타입 시스템 - 잘못되지 않는 모든 프로그램들을 받아들이는 시스템 - 에 비춰볼 때 타입 세이프하다고 할 수 있습니다. 이 결론은 이상해 보일 수 있습니다. Java에서 o.m()이 잘 타이핑 되었다면 그건 o라는 객체가 m이라는 인자가 없는 메소드를 갖는다는 것을 보장하기때문에, 이 호출은 항상 성립할 것입니다. 하지만 루비에선 o.m()은 항상 루비의 (null) 타입 시스템에 의해 잘 타이핑되었음이 보장되었더라도, o 라는 객체가 m이라는 함수를 가지고 있는지, 그리고 그 호출이 성공적일지 단언할 수 없습니다. 타입 안정성은 하나로 정의될 수 없습니다. 타입 안정성이 보장하는것은 각 언어에서 무엇이 잘못된 행동인지를 정의하는 의미론에 따라 다릅니다. 자바에서는 존재하지 않는 함수를 호출하는 것이 틀렸지만, 루비에선 예외를 던질 뿐 틀린 건 아닙니다.

기본을 넘어서

제너릭 타입 안정성은 유용합니다.

한편으론, 루비와 자바의 예시에서도 알 수 있듯 모든 타입 시스템이 같지는 않습니다. 어떤 언어는 보장할 수 없는 성질들을 다른 언어는 보장합니다. 따라서 어떤 언어가 타입 세이프한지 묻는 것보다 중요한 것은 타입 세이프함이 어떤걸 가능케 하는지입니다. 타입 시스템이 할 수 있는 몇가지 예시들을 알아보겠습니다.

간극 줄이기

저 위의 벤다이어그램에서 잘 타이핑된 (well-typed) 부분과 잘 정의된 (well-defined) 부분은 일치하지 않습니다. 그 차집합에는 잘 정의되어 있지만 타입 시스템이 수용하지 않는 코드들이 있습니다. 예를 들어 대부분의 타입 시스템은 아래의 프로그램을 허용하지 않을 것입니다.

if(p) x = 5;
else x = "hello";

if(p) return x+5;
else return strlen(x);

위의 코드가 integer를 반환하더라도, 타입 시스템은 변수 x가 int도, string도 될 수 있기 때문에 잘못되었다고 말할 것입니다. 정적 분석에서 예시를 들어보자면, Heartbleed bug에서도 논의 되었듯, 타입 시스템은 좋지만 완벽하지 않습니다. 이 불완전성이 많은 프로그래머들을 당황시키는 동시에 파이썬이나 루비로 뛰어들게만드는 이유입니다. 더 많은 프로그램들을 수용할 수 있는, 간극을 줄이는 타입 시스템을 디자인하는 것이 해결책일 것입니다.

Invariant를 강제하기

전형적으로 프로그래밍 언어는 int나 string같은 타입을 가지고 있습니다. 타입 안정성이란 int가 실제로 int임을 보장하는 것을 말합니다: int 안의 값이 -1, 2, 47인지를 런타임에 알고 적용하는 것이죠. 하지만 int에 머물러 있을 필요는 없습니다. 타입시스템은 훨씬 더 풍부한 타입을 지원할 수 있고 프로그램 표현에 있어 더 흥미로운 속성들을 가질 수 있게 합니다.

최근들어 논리식을 통해 타입의 가능한 값들을 지정하는 refinement types에 대한 관심이 증가하고 있습니다. 타입 {v:int

0<=v>}는 int 타입을 0 <= v 라는 식으로 제한해서 음수가 들어올 수 없도록 합니다. Refinement 타입은 데이터 구조의 불변값(invariants)들을 그 데이터 구조의 타입으로 나타낼 수 있게 함으로써, 불변값들의 타입 안정성이 항상 성립하도록 도와줍니다. Refinement 타입 시스템은 하스켈이나 F#(liquid Haskell) 혹은 다른 언어들에게서 개발되었습니다.

다른 예시로는, 타입 시스템은 데이터 교착문제 (data racing)로부터 자유를 줄 수 있습니다. 불변값들에 대해, 공유된 변수가 변수를 가드하는 락을 소유한 하나의 쓰레드에 의해서만 접근가능하도록 강제함으로써 말입니다. 공유 변수의 타입은 그걸 보호하는 lock을 나타냅니다. 이와 같은 Types for safe locking은 Abadi와 Flanagan에 의해 최초로 제안되었습니다.

타입 추상화와 정보 은닉

많은 프로그래밍 언어는 개발자들에게 정부 추상화(은닉)를 권장합니다. 이들 언어들은 클래스, 모듈, 함수 등의 추상화를 통해 클라이언트 코드로부터 내부 로직에 대한 정보를 감출 수 있게 합니다. 클라이언트단의 코드를 수정하지 않고도 내부 동작이 수정될 수 있기 때문에, 추상화를 적절히 사용하는 것은 좀 더 튼튼하고 유지보수가능한 프로그램을 만듭니다. 타입 시스템은 이 추상화를 강제하는데 중요한 역할을 할 수 있습니다. Representation independence란, 프로그램들은 그것이 어떻게 구현되었나와는 관계없이, 추상화단에서의 동작에만 의존해야 한다는 개념인데, 이는 잘 구현된 타입 시스템에 의해 큰 도움을 받을 수 있습니다. Wadler는 타입에 의한 강제된 추상화가 [free theorems]을 가능케한다는 것이 밝힌 적 있습니다. 1983년 John Reynolds는 Types, Abstraction, and Parametric Polymorphism에서 타입과 추상화에 대한 놀라운 성과를 이룩했습니다. 이 논문에서 그는 타입 구조는 추상화 계층을 유지하기위한 문법적 규칙이다 라고 주장했습니다.

맺음말

타입 안정성은 중요합니다. 타입 세이프한 언어들은 프로그램이 잘 정의되었음을 최소한 보장합니다. 보안이 중요한 상황에서는 프로그램이 무엇을 할 수 있을지를 아는것이 매우 중요하기 때문에, 이것(well-defined)이 보장되는 것이 필수입니다. 하지만 타입 시스템은 이것 외에도 프로그램의 근본적인 논리구조에도 영향을 미치고, 불변값을 쓰도록 강제하고, 추상화를 관리할 수 있도록 해줍니다. 소프트웨어가 갈수록 복잡하고 널리 쓰이게 될 수록, 타입 시스템은 우리가 사용하는 소프트웨어가 신뢰할 수 있고 안전하다는 것을 보장하는 중요한 도구가 될 것입니다.